Generalised LL (GLL) parsing is a practical technique of parsing general context-free grammars. Gogll is an open source compiler kit that generates a GLL parser and a finite state automaton (FSA) based lexer for any context-free grammar. Gogll generates code in Go and Rust.
What is GLL?
Generalised LL (GLL) parsing [Scott 2010,2012] is a parsing technique that that can handle any context-free grammar. It parses from left to right and produces a parse forest containing all valid parse trees.
Most well-known parsing techniques, such as: LL(1)/LL(*) (ANTLR), LALR (Yacc) or LR(1) (gocc), handle only a subset of context-free grammars and can fail unpredictably when hidden left recursion occurs in the grammar. Generalised LR (GLR) parsers [Grune 2008] also handle all context-free grammars but are more complex to implement than GLL.
Ambiguous grammars can produce an unbounded polynomial number of derivations for certain input strings (see Ambiguity and Parse Forests below). GLL represents these derivations in a binarised shared packed parse forest (SPPF) [Scott 2012], which has worst-case cubic space complexity. The time and space complexity of the GLL algorithm is worst-case cubic in the length of the input string and linear for LL productions [Scott 2012].
What is GoGLL?
Gogll is an open source compiler kit that generates a GLL parser and its companion finite state automaton (FSA) based lexer for any CF grammar. Gogll supports Go and Rust as target languages for code generation.
For syntactically valid input strings the parser returns a version of SPPF, called a binary subtree representation (BSR) set [Scott 2019]. The BSR set can be walked recursively and disambiguated by preferentially selecting subtrees (see Disambiguating the Parse Forest below).
Why do we need GLL?
- General context-free (CF) grammars often require fewer symbols than LR(1) or LL(1) grammars to express the same language.
The following excerpt is from a real query language, which was first implemented in LR(1) and then redone as a CFG using gogll. In the LR(1) grammar parentheses was required around several expressions like the one in the production shown below to prevent LR(1) conflicts:
LR(1):
======
RangeExpr :
...
| "(" LTRangeExpr "|" GTRangeExpr ")"
...
;
In the context-free grammar the parenthesis could be omitted, simplifying the language to:
CFG:
===
RangeExpr :
...
| LTRangeExpr "|" GTRangeExpr
...
;
- LL parsers cannot handle immediate left recursion:
A -> Aβ[Grune 2008]. When a grammar is rewritten to remove immediate left recursion it is often less readable than the original CF grammar and the syntax of the language can be obscured.
Grammar G1, below, is a valid context-free grammar but is obviously left
recursive and therefore cannot be handled by an LL parser.
G1
==
E : E "&" E
| E "|" E
| id
;
-
Hidden left recursion [Grune 2008] occurs in a grammar if a production
Acan derive a stringβAμin 0 or more steps andβcan derive the empty string in one or more steps:A =>* βAμ, β =>+ ε. Neither LL nor LR parsers can handle hidden left recursion, which can be very indirect and hard to spot in a grammar. -
LR parsing tables can be exponential in the size of the grammar.
-
Look-ahead of more than 1 is tricky [Grune 2008] in LL(k>1) and LR(k>1) parsers and leads to very large parse tables.
-
Neither LL(k) nor LR(k) grammars can handle ambiguous grammars (such as
G1above). An attempt to generate an LR-1 parser forG1results in shift-reduce conflicts.
But an ambiguous context-free grammar often gives the most natural definition
of the intended language.
For example: G1 gives a very natural definition of simple boolean logic
expressions (ignoring operator precedence). The grammar is ambiguous and can produce multiple valid parse trees for the
same input string, not all of which will be logically valid. We will see later on
how to deal with this ambiguity in gogll.
The following grammar, G2, has been rewritten from G1 to encode
the precedence of the logic operators in the grammar.
We can generate an LR(1) parser for this grammar, which
will produce a single logically valid parse tree for any syntactically
valid input string.
G2
==
E : E "|" T
| T
;
T : T "&" id
| id
;
The following grammar, G3, has been rewritten from G2 to remove
left recursion. An
LL(1) parser can be written or generated for G3. A G3 parser would also
produce only one logically valid parse tree for any syntactically valid
input string, but it is even harder to understand than G2.
G3
==
E : T E1 ;
E1 : "|" E1
| ε
;
T : id T1 ;
T1 : "&" id
| ε
;
- Context-free grammars are composable, meaning that the composition of 2 or more CF grammars is another CF grammar. But CF subsets, such as LL(k) or LR(k) are not composable in general. So GLL allows modular composition of grammars, something that gogll aims to support in a future version.
Ambiguity and Parse Forests
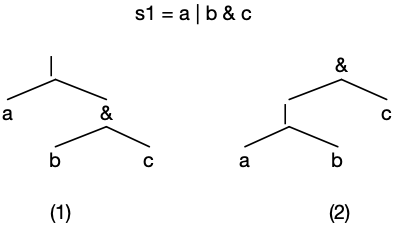
A GLL parser for G1 will produce the following two syntactically valid
parse trees for the input string, s1 = a | b & c:
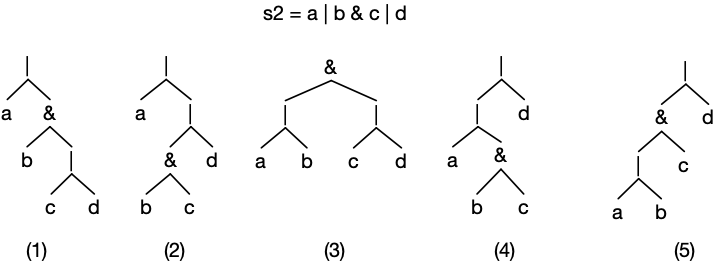
The same parser produces the following five syntactically valid parse trees for the input string, s2 = a | b & c | d:
In general the number of parse trees for G1 grows as an unbounded polynomial
of the number of operators (&||) in the input string.
The number of parse trees for a string with n operators is given by the
Catalan number C[n].
See [Knuth 2011] for a detailed analysis of finding all the parse trees.
The Catalan numbers grow very fast so that the parser for G1 will produce
C[19] = 1 767 263 190 parse trees for the following input string:
s3 = a1 & a2 | a3 & a4 | a5 & a6 | a7 & a8 | a9 & a10 | a11 & a12 | a13 & a14 | a15 & a16 | a17 & a18 | a19 & a20
The GLL parsing technique uses a binarised shared packed parse forest [Scott 2012] to represent the valid parse trees. This technique restricts the space complexity of the parse forest produced by a GLL parser to worst-case cubic in the length of the input.
Disambiguating the Parse Forest
After successfully parsing an input string we usually have to disambiguate the parse forest to produce a single parse tree or abstract syntax tree, which is used for further processing.
It is straight-forward to disambiguate the parse forest while walking it [Afroozeh 2015].
Consider again the valid parse trees for G1 and string s1 = a | b & c:

Parse tree (1) is logically valid because & is evaluated before | but
parse tree (2) is logically invalid because | is evaluated first. We can
easily disambiguate this forest by rejecting all trees with a & node
above a | node; or in other words:
reject all trees in which a parent node has
precedence over a child node, given the precedence relation for G1:
id > & > |
Applying the precedence rule to the parse trees for G1 and the input string
s2 = a | b & c | d:

means that we accept parse trees (2) and (4): the only logically valid parse trees in the forest. If we require only one parse tree we could pick any of the logically valid trees because all are equivalent representations of the same logical expression.
Additional rules could be applied, for example: to distinguish between identifiers and reserved words of a language; or other sources of ambiguity.
See
gogll examples/g1
for Go
and Rust
implementations of the operator precedence disambiguation rule for G1.
The implementations choose the first logically valid parse tree encountered while
traversing the parse forest.
Complexity and Performance
How concerned should we be about the complexity and performance of GLL parsers,
given that the simple grammar G1 can produce 1 767 263 190 parse trees for input
s3?
Scott and Johnstone proved [Scott 2012] that the space and time complexity of GLL is worst-case cubic in the number of input tokens and linear for LL productions.
In the case of G1 and s3 the 1 767 263 190 parse trees are represented
in only 1369 non-terminal BSR nodes in the SPPF of the parser generated by gogll.
To measure the time performance gogll was used to generate both a
Rust and Go version of the lexer and parser
for G1.
The disambiguation rule based on operator precedence, explained above, was implemented
in Go and Rust and the first logically valid parse tree is selected.
The BSR set implementation of the SPPF generated by gogll uses a hash set for non-terminal nodes. Each run of the parser on the same input therefore generates a forest containing the same parse trees but in random order. The number of nodes to walk in order to find the first valid parse tree therefore varies from run to run resulting in the variance in the treewalk measurements below. Both implementations were run 10 times to produce the following time measurements:
| Go Parse | Go Treewalk | Rust Parse | Rust Treewalk | |
|---|---|---|---|---|
| Avg | 2.4 ms | 2_808.8 ms | 3.6 ms | 1_040.5 ms |
| Min | 2.3 ms | 6.1 ms | 3.0 ms | 5.6 ms |
| Max | 2.6 ms | 7_258.8 ms | 4.0 ms | 3_065.1 ms |
- Parse is measured from after lexing is complete until the BSR set is returned by the parser.
- Treewalk involves walking the parse forest until the first parse tree is found
that is valid under the precedence rule (
id > & > |).
From the above it is clear that the Rust and Go GLL parsers generated by gogll are not only feasible for terrible worst cases, but practical and fast in real terms.
History
The signature achievement of Computer Science is the theory of Computation (see [Sipser 2013] for a comprehensive introduction), comprising: automata and languages; computability theory; and complexity theory.
The quest for practical parsing algorithms for context-free languages led to the landmark 1965 paper by Knuth [Knuth 1965] on LR(k) languages.
De Remer invented LALR parsing in 1969 [De Remer 1969] and published an algorithm to generate the lookahead sets in 1982 [De Remer 1982].
David Pager’s beautiful paper on his Practical General Method for Generating LR(k) Parsers (PGM) appeared in 1977 [Pager 1977].
These two techniques, LALR and PGM, reduced the size of LR(1) parsing tables sufficiently to make LR parsing practical on the hardware of the time. Together with LL(1), LALR and LR(1) have remained the primary workhorses of parser writers.
Much work was done in the following years to find practical parsing algorithms for more general context-free languages. An excellent source for parsing up to and including generalised LR is by Grune and Jacobs [Grune 2008].
In the mean time most parser writers either hand crafted an LL(1) parser or used tools such as ANTLR (LL(1)/LL(*)), Yacc (LALR) or gocc (LR(1)) to generate parsers.
In 2010 Scott and Johnstone published a practical algorithm for generalised LL (GLL) recognition [Scott 2010], which could handle all context free grammars. Their 2012 paper [Scott 2012] describes GLL parse-tree generation, which is necessary for a functional parser. In a 2019 paper with Van Binsbergen [Scott 2019] they described a variant of the GLL algorithm that represents the parse forest as a set of binary subtrees.
For many years I have disliked the ad hoc conflict resolution required to parse practical languages with a single token look-ahead, be it by LL(1) or LR(1). In 2019 I implemented a GLL parser generator for the [Scott 2019] technique. This compiler generator, which also generates a linear-time FSA lexer for the tokens of the same grammar, is available as open source (gogll). Since 2020 gogll generates code for both Go and Rust.
Definition of Terms
| Term | Definition |
|---|---|
| BSR | Binary subtree representation (of an SPPF) [Scott 2019] |
| CF | Context-free (grammar or language) |
| CFG | Context-free grammar |
| CFL | Context-free language |
| GLL | Genereralised LL parsing [Scott 2010,2012,2016,2019] |
| SPPF | Shared packed parse forest [Scott 2012,2019] |
Bibliography
The following are my copies of this literature. More up to date versions may be available for some.
-
[Afroozeh 2015] Ali Afroozeh and Anastasia Izmaylova
One parser to rule them all
In: 2015 ACM International Symposium on New Ideas, New Paradigms, and Reflections on Programming and Software (Onward!) -
[ANTLR] Terence Parr. ANTLR (ANother Tool for Language Recognition). https://www.antlr.org.
-
[De Remer 1969] Franklin L. DeRemer, (1969)
Practical Translators for LR(k) languages
Ph.D thesis MIT 1969 -
[De Remer 1982] Frank DeRemer and Thomas Pennello
Efficient Computation of LALR(1) Look-Ahead Sets” (PDF)
ACM Transactions on Programming Languages and Systems. 4 (4): 615–649 (October 1982) -
[gogll] Marius Ackerman
Gogll. A compiler kit that generates GLL parsers with FSA lexers for Go and Rust.
https://github.com/goccmack/gogll 2020 -
[Grune 2008] Dick Grune and Cerial J.H. Jacobs.
Parsing Techniques. A Practical Guide.
Monographs in Computer Science. Second Edition.
Springer 2008. -
[Grune 2012] Dick Grune, Kees van Reeuwijk, Henri E. Bal, Ceriel J.H. Jacobs and Koen Langendoen.
Modern Compiler Design. Second Edition.
Springer 2012 -
[Knuth 2011] Donald E. Knuth
The Art of Computer Programming Volume 4A / Combinatorial Algorithms, Part 1 Section 7.2.1.6. Generating all trees Pearson Addison Wesley 2011 -
[Pager 1977] David Pager
A Practical General Method for Generating LR(k) Parsers
In: Acta Informatica 7, 249–268 (1977) -
[Scott 2010] Elizabeth Scott and Adrian Johnstone.
GLL Parsing.
In: Electronic Notes in Theoretical Computer Science 253 (2010) 177–189 -
[Scott 2012] Elizabeth Scott and Adrian Johnstone. GLL parse-tree generation
Science of Computer Programming 2012 -
[Scott 2016] Elizabeth Scott and Adrian Johnstone.
Structuring the GLL parsing algorithm for performance.
In: Science of Computer Programming Volume 125, 1 September 2016 -
[Scott 2019] Elizabeth Scott, Adrian Johnstone and L. Thomas van Binsbergen.
Derivation representation using binary subtree sets.
In: Science of Computer Programming (175) 2019 -
[Sipser 2013] Michael Sipser.
Introduction to the Theory of Computation. Third edition.
CENGAGE Learning 2013.